[retour à la page principale | page précédente | page suivante ]

Chapitre VII: SYSTÈMES LINÉAIRES

A- Généralités

Tout système linéaire peut être représenté sous forme matricielle. La résolution d'un tel système fait appel à la notion d'inverse d'une matrice.

B - Exercice résolu

Considérons le système d'équations suivant:
Ce système peut être écrit sous une forme matricielle: AX = B, avec:
Résoudre ce système d'équations, c'est trouver X tel que AX = B.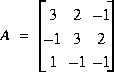

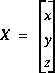
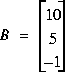
MATLAB permet de résoudre ce problème en écrivant les instructions suivantes:

   A = [3 2 -1;-1 3 2;1 -1 -1];

   B = [10 ;5 ;-1];

   X = inv(A)*B
On obtient comme résultat:

  X =

    -2.0000

     5.0000

    -6.0000

  >>

Note: on peut aussi utiliser la commande MATLAB

   X = A\B

C- Exercices

Résoudre les systèmes d'équations ci-dessous en utilisant 

 
   X=inv(A)*B
et 
 
   X=A\B
Pour les sytèmes d'équations à deux inconnues, faire également la résolution graphique à l'aide de MATLAB. Pour les systèmes qui admettent plusieurs solutions, donner une interprétation graphique.

 VII.1 

         


           


 

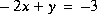
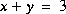
 VII.2  

        


        


 

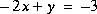
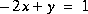
 VII.3  

       


       


       


 

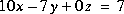
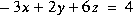
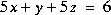
 VII.4

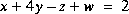
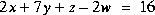
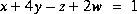
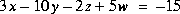
[retour à la page principale | page précédente | page suivante]