- Techniques du driver de recherche
du meilleur seuillage possible -
Version 1.01 -
- Par:
Romain Dubois & Matthieu Klein
Le but est de trouver automatiquement, le meilleur seuillage possible de l'image de la caméra. Il s'agit donc d'un autocalibrage. Nous allons ainsi tenter de mettre en évidence la méthodes et les concepts - que l'on expliquera - sur lesquels nous nous appuyons. Les mots clés de cet article sont: entropie, compression de données, liens entre compression et entropie, interprétation des graphiques.
Introduction
Mesure de la qualité
d'une image
Mesure de la quantité
d'information dans les images par compression
Application aux images
du labyrinthe
Relations entre histogrammes
de luminescences et entropie
En conclusion
Le seuillage fait
rapidement varier l'image en fonction de la lumière à laquelle
est exposé le labyrinthe. Lorsque le seuillage est trop élevé,
on obtiendra une image couverte superficiellement ou intégralement
de tâches plus ou moins bien définies. Si le seuillage est
trop faible, l'image recueillie sera très blanche, au point même
de dissoudre certaines zones du labyrinthe. Des parties de murs peuvent
disparaitre entièrement. Il existe entre ces 2 cas, un seuillage
idéal que nous voulons trouver automatiquement.
Mesure de la qualité d'une image
Définition
d'une image de bonne qualité: les pixels blancs doivent se trouver
le plus possible sur les chemins et autour du labyrinthe, alors que les
points noirs doivent se trouver le plus possible sur les murs noirs du
labyrinthe. Les points noirs se trouvant au milieu de zones blanches et
les points blancs se trouvant dans les murs noirs provoquent du désordre,
et engendrent donc une augmentation de l'entropie, c'est-à-dire
une augmentation de la quantité de désordre.
Plus il y a de désodre, moins il y a de redondances et plus
l'entropie est élevée. De plus, si le désordre est
élevé, il est difficile de définir l'image, puisqu'elle
contient beaucoup de points qui n'ont pas de relations entre eux-même
(bruits). Ainsi, la quantité d'information pour définir
une image où il y a du désordre est élevée.
On rentiendra dès lors que hausse du désordre
= hausse de l'entropie = hausse de la quantité d'informations
= baisse de la redondance = hausse de la taille du fichier si
on désire le compresser.
Une image vide, blanche, se compresse très bien, car la quantité
d'information contenu dans l'image est proche de 0. D'une autre manière,
le résultat de la taille du message comprimé peut être
directement assimilié à la valeur d'entropie topologique
de l'image.
Mesure de la quantité d'information dans les images par compression
La théorie
de l'information définit la quantité d'information d'un message
(i.e un fichier texte, une image etc..) comme le nombre minimum
de bits nécessaires pour coder toutes les significations possibles
de ce message. Un exemple de calcul d'entropie très simple en http://www.hrnet.fr/~matthieu/crypto/5.htm#5.1
aide à bien cerner ce que représente cette entité.
Cela évoque la définition d'un compresseur de données.
La finalité d'un compresseur comme Zip, Rar ou Arj est de réduire
la taille d'un message au minimum, sachant que la quantité d'infomation
contenue dans le message réduit (par compression sans pertes) sera
identique à la quantité d'information utile du message
ogirinal. Idéalement, le fichier compressé ne devrait contenir
que des informations utiles. On sait aussi qu' une séquence aléatoire
qui est équiprobable (donc non redondante, comme dans le fichier
après une compression), tel qu'il à été expliqué
en cours,
représente la quantité d'information maximum. Un message
ne peut pas contenir plus d'informations que sa taille ne lui permet. Il
vient alors que la quantité d'information maximum d'un message,
est la taille même de ce message. Cela démontre que la taille
d'un message idéalement compacté, représente directement
la valeur de l'entropie du message. Plus présisement, il s'agit
là de la mesure d'entropie topologique, qui utilise les redondances
formelles internes au message. Dominique Revuz explique
cette entropie dans sa thèse d'informatique fondamentale sur
les dictionnaires et lexiques d'un texte.
Nous savons donc quantifier facilement le désordre dans les images
simplement à l'aide du compresseur de données. L'avantage
réside dans la fait que des algorithmes de bons compresseurs (sans
pertes) se trouve très facilement. Notre driver dispose ainsi d'une
routine de compression Lempel-Ziv, dont l'algorithme a été
élaboré en 1977 par Lempel et Ziv. (Le mot "Zip" de PkZip,
provient de Ziv. Pkzip utilise cet algorithme, en plus d'une précompression
de Huffman). La routine du driver comprime l'image en mémoire, recupère
uniquement la taille, puis jette l'image comprimée. Nous ne disposons
pas de routines de décompression, cela ne nous intéresse
pas dans le cadre de cette application.
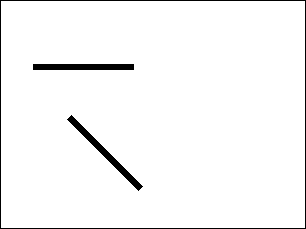
Voici 3 images. Chaque image représente 2 rectangles de même
longueur. Nous les avons soumises toutes les 3 à notre driver pour
en extraire leur entropie (taille après compression)

|

|
|
- Le 1er dessin, les 2 rectangles (qui n'en forme qu'un) sont très bien ordonnés, l'un a coté de l'autre et bien contre le bord. La quantité d'information est très faible et tient en 498 octets.
- La 2ieme image est identique à la première, sauf que les 2 rectangles sont déplacés. Cette image est donc à peine moins bien rangée que la 1ere, puisque le rectangle se trouve non plus contre le bord, mais au milieu de l'image. Il y a a donc plus d'information. Son entropie s'éléve immédiatement et vaut 515 octets.
- La 3ieme image représente ces 2 rectangles disposés à 45 degrés l'un par rapport à l'autre.Les rectangles sont bien moins ordonnés que dans les 2 images précédentes. Il est donc plus difficile de décrire cette image, ce qui signifie qu'il faut plus de paramètres, donc plus d'informations pour la définir. Cela se traduit encore une fois, par une hausse de l'entropie, passant à 636 octets.
Application aux images du labyrinthe:
Sur le même
principe, l'on mesure chacune des entropies pour l'image de la caméra,
avec les 255 seuillages différents. On a donc 255 images seuillées
différentes, soit 255 compressions de message à faire. Ci-après,
les graphes réels, d'après les valeurs données par
le compresseur du driver. (le driver retourne également la dérivée
des courbes):
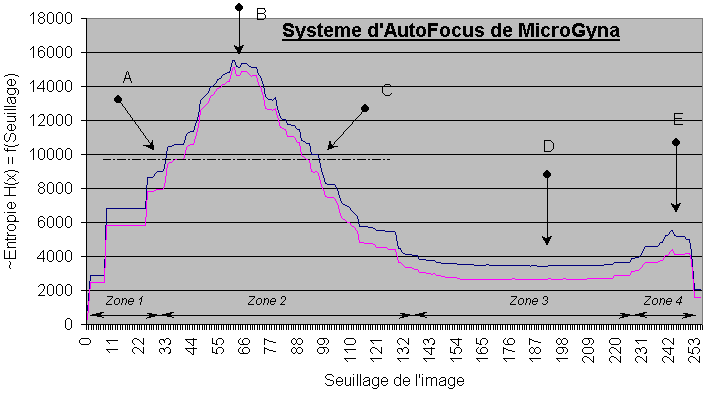
La courbe bleue est celle d'une série d'images au format RAW enregistrée sur disque, que le driver interprète dans son mode de simulation. Le format Raw stoque 1 pixel par octet. De plus un pixel est blanc ou noir, donc il est codé sur 1 bits. Cela signifie que 7 bits par octets ne sont pas utilisés. La courbe rouge représente la même série d'images, mais codée avec 8 pixels par octets. Elle prend donc en mémoire, avant la compression, 8 fois moins de place que le format Raw. Le but est de montrer que les 2 résultats sont presques identiques. On montre que la compression n'est pas fonction de la taille du fichier d'entrée. Elle est fonction de l'information contenue dans l'image. Que l'image soit formattée en Raw ou dans un autre format, même Gif, elle dispose de la même entropie.
Analysons les 4 zones du graphique ci-dessus:
- La zone 1 montre une zone de mauvaise sensibilité de la caméra. La résolution de cette caméra est légèrement inférieure à 8 bits (le graphique s'étale sur 8 bits, de 0 à 255 seuillages en luminosité)
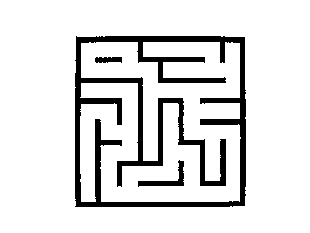
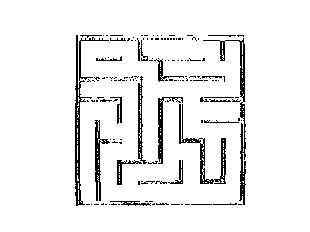
- La zone 2 est une zone de grande sensibilité dans les niveaux de gris clairs. Dans cette zone, pour un seuillage à peine plus élevé, le chaos dans l'image augmente vite. Cela est lié au fond de l'image qui varie dans les niveaux de gris clairs. Ci dessous, les images obtenues aux points A, B, C. Notons le point B. C'est à ce niveau de seuillage que l'image à le plus d'entropie, c'est donc à ce niveau qu'elle est le plus en désordre. L'image B ci dessous témoigne effectivement d'un grand nombres de points aléatoires. Les images A et C disposent de la même entropie (donc de qualité égale), à des valeurs de seuillage différent.
- La zone 3 est la zone clé. Elle montre d'une part une longue stabilité, et d'autre part, une entropie très basse, la plus basse entre les 2 maxima locaux. Dans cette zone, l'image est la plus nette possible, et elle ne contient que de l'information liée à la structure du labyrinthe. Les pixels noirs sont à leur place, comme les pixels blancs. Il existe ailleurs sur la courbe des points d'entropie plus bas, car pour certain seuillage extrême, les images ne disposent de pratiquement plus aucune information, tant elle est recouverte de points de même couleurs.
- La Zone 4 montre de nouveau une augmentation du désodre. Des points blancs viennent "ronger" les murs. La hauteur de ce 2 ième maximum local est fonction de l'épaisseur des murs du labyrinthe. Si les murs était très épais, l'entropie serait plus élevée, puisque nous aurions beaucoup de points blancs, dans beaucoup de surface noire. C'est le phénomène inverse qui produit la 1ere grande bosse, puisque il y a plus d'espace blancs que de murs noirs.
 |
 |
 |
 |
 |
|
Le graphe suivant montre la dérivé associée à
la fonction entropique, pour une autre image de labyrinthe. Cette dérivée
est retournée également dans un tableau mémoire, par
le driver. On constate que la zone stable est bien plus grande que sur
le graphe précédent. Le fait qu'il semble moins bruité,
n'est qu'une impression provoquée par un choix d'échelle
plus petite.
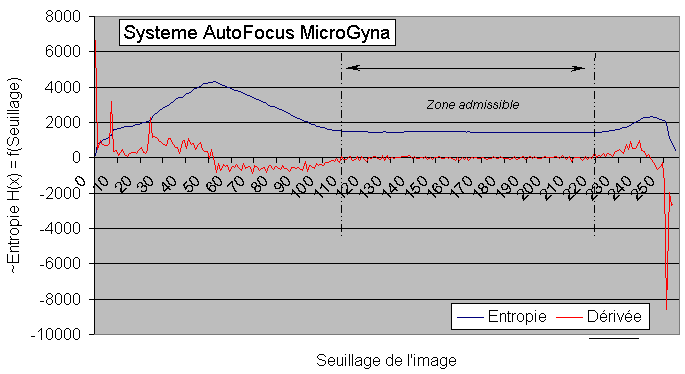
Le driver calcul la dérivée pour trouver la zone idéale.
On comprend on voyant l'allure de la dérivée, que l'analyse
numérique pour en extraire le meilleur seuillage est un défi
de taille. Pour cette image, le driver calcule que le meilleur seuillage
en 167. Ce résultat est excellent, mais l'analyse risque de ne plus
fonctionner pour des images sur ou sous exposées. Une image sous
ou sur - exposée en lumière va engendrer un graphique décalé,
le laissant appraître uniquement l'un ou l'autre des maxima locaux.
Nos algorithmes se basent pour le moment sur le fait qu'il y a 2 maxima
locaux. L'autocalibrage ne fonctionnera donc pas, sauf si l'on récrit
des routines d'analyses pour les cas de mauvaises expositions. Ces algorithmes
sont en projets.
Relations entre histogrammes de luminescences
et entropie:
Il existe une certaine
relation entre ces 2 mesures. En effet, le premier maximum local de l'entropie
du graphique ci-dessus, correspond à la moitié de la création
de l'objet "fond d'écran". L'objet n'étant définit
qu'à moitié, c'est à cet instant qu'il est le plus
chaotique, d'ou une entropie excessivement élevée. Nous pourrions
aussi dire que la moitié de la définition du fond de l'écran,
correspond à la mise en place de la moitié des points constituant
l'objet fond, correspondant encore à la moitié des points
de couleurs de luminosité inférieure ou égale à
la couleur de luminosité principale de l'objet. Or, la couleur principale
de l'objet est par définition la couleur la plus prononcée,
donc celle qui correspond au maximum local de l'histogramme luminescence
(ou de niveaux de gris). Par exemple, l'histogramme de l'image 8 bits du
labyrinthe utilisée pour calculer le graphique d'entropie ci-dessus
est le suivant:
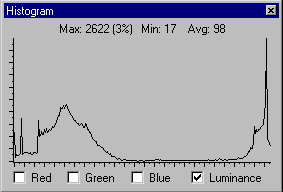
On retrouve les grands traits, qui sont les grands maxima locaux, correspondants
respectivement au fond blanc de l'écran (zone large) et aux murs
du labyrinthe (zone étroite).
En conclusion
Nous pouvons dire
que l'approche par l'entropie pour l'autocalibrage est intéressante,
dans la mesure où elle est facile à calculer, et où
elle donne des résultats facile à interpréter intuitivement
et logiciellement. Son défaut réside dans la lenteur du calcul,
bien qu'il soit facile de changer d'algorithme pour passer de Lempel-Ziv
à du RLE par exemple, plus rapide. Le calcul d'entropie est suffisament
sensible pour que l'on obtiennent des graphiques pertinents avec des images
de très basses qualités. Si nous avions eu a traiter directement
des flots d'images 8 bits, une analyse par histogrammes aurait été
un bon choix.