


Toute donnée peut être représentée sous forme matricielle. En effet, une donnée constituée d'une valeur numérique est une matrice uniligne unicolonne. Un ensemble de quatre coordonnées dans un repère 0xyz peut se représenter avec une matrice ayant quatre lignes et trois colonnes etc..
Pour spécifier un élément dans une matrice, on utilise le numéro de la ligne et celui de la colonne.
Par exemple, soit une matrice C donnée. C_43 = 2 signifie que le nombre situé à la quatrième ligne et deuxième colonne de la matrice C est égal à 2.
Une matrice m*n est une matrice qui à m lignes et n colonnes.
On obtient la taille d'une matrice en faisant le produit du nombre de lignes par le nombre de colonnes.
Une matrice est dite carrée si le nombre de lignes est égal au nombre de colonnes.
Initialisation de matrices en utilisant MATLAB
Dans une fenêtre MATLAB on écrit ce qui suit:
>> A = [1 2 3;4 5 6;7 8 9]On obtient comme résultat une matrice 3X3:
A =On peut concaténer deux ou plusieurs matrices.1 2 3
4 5 6
7 8 9
Exemple:
>> R = [10 11 12];
>> B = [A;R]
On obtient comme résultat:
B =On peut initialiser une matrice avec un énoncé.
1 2 3
4 5 6
7 8 9
10 11 12
Exemple:
>> C = [-0.4 pi sqrt(-3)]On obtient comme résultat:
C =-0.4000 3.1416 0 + 1.7321i
Une matrice peut être initialisée en utilisant d'autres matrices (associations par blocs de matrices).
Exemple:
>> D = [A,zeros(3,2);zeros(2,3),eye(2)]
On obtient comme résultat:
D =
1 2 3 0 0
4 5 6 0 0
7 8 9 0 0
0 0 0 1 0
0 0 0 0 1
D est une matrice 5X5 dont les 3 premières lignes et les 3 premières colonnes sont la matrice A vue précédemment. Les 3 premières colonnes des lignes 4 et 5 sont des zéros: matrice zeros(3,2). Les 3 premières lignes des colonnes 4 et 5 sont également des zéros: zeros(2,3). La matrice carrée identité eye(2) constitue les lignes et colonnes 4,5.
Soit les matrices
A = [2 5 1;0 3 -1] B = [1 0 2;-1 4 -2;5 2 1] et D= [2 1;4 3]On se propose de calculer :
a - Les transposées de A et B.
b - Le produit de A par B noté C
c - La taille de C
d - L'inverse de D
e - Le carré des éléments des matrices A B et D
Considérons les énoncés MATLAB suivants.
On obtient les résultats suivants:A =[2 5 1;0 3 -1];
B = [1 0 2;-1 4 -2];
D = [2 1;4 3];
A'
B'
D'
C = A.*B
size(C)
inv(D)
A.^2
B.^2
C.^2
Transposée de A
ans =
2 0
5 3
1 -1
Transposée de Bans =
1 -1
0 4
2 -2
Transposée de Dans =
2 4
1 3
Le produit de A par BC =
2 0 2
0 12 2
La taille de Cans =
2 3
L'inverse de la matrice Dans =
1.5000 -0.5000
-2.0000 1.0000
Le carré des élèments de la matrice Aans =
4 25 1
0 9 1
Le carré des élèments de la matrice Bans =
1 0 4
1 16 4
Le carré des élèments de la matrice C
ans =
4 0 4
0 144 4
>> Quelques remarques à propos de l'exercice résolu :
- La transposée d'une matrice est une nouvelle matrice dans laquelle les lignes de la nouvelle matrice sont les colonnes de l'ancienne tandis que les colonnes de la nouvelle sont les lignes de l'ancienne.
- L'inverse d'une matrice ne peut être obtenue qu'à partir d'une matrice carrée.
- En faisant A.^ 2. A étant une matrice, on obtient une nouvelle matrice dans laquelle chaque élèment est obtenu en élevant au carré chaque élèment correspondant de la matrice de départ.
- Si on veut obtenir le produit d'une matrice A par elle-même, on fait A^2.
- Pour faire le produit de deux matrices A(m,n) et B(m',n') il faut s'assurer que n = m'.
V - Soit les matrices ci-dessous:
Utiliser MATLAB pour définir ces matrices, puis calculer: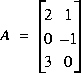
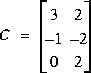
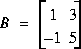
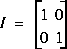
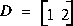
V.1 - AB
V.2 - DB
V.3 - BC'
V.4 - (CB)D'
V.5 - B-1
V.6 - BB-1
V.7 - B-1B
V.8 - AC'
V.9 - (AC')-1
V.10 - (AC')-1 AC'
V.11 - IB
V.12 - BI

[retour à la page principale | page précédente | page suivante]