


Graphiquement, la dérivée d'une fonction peut être définie comme la pente de celle-ci à un point donné.
La différentiation numérique consiste à calculer la dérivée d'une fonction en un point xk:
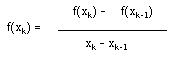
Considérons la fonction suivante
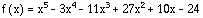
On se propose de :
- Représenter cette fonction entre -4 et 5.
- Calculer sa dérivée par rapport à x.
- Représenter cette dérivée.
- Determiner les valeurs de x pour lesquelles la fonction f(x) admet des maxima et des minima locaux.
En MATLAB, on écrit les instructions suivantes:
Partie 1
x = -4:0.1:5;
f = x.^5 - 3*x.^4 - 11*x.^3 + 27*x.^2 + 10*x -24;
figure;plot(x,f,'+')
title(' f = x^5 - 3x^4 - 11x^3 + 27x^2 + 10x - 24')
xlabel('abscisse')
ylabel('ordonnés')
grid
hold
Partie 2
df = diff(f)./diff(x);
xd = x(2:length(x));
figure;plot(xd,df)
title('dérivée de la fonction f')
xlabel('abscisse')
ylabel('ordonnés')
grid
Partie 3
produit = df(1:length(df)-1).*df(2:length(df));
local = xd(find(produit<0))
On obtient les figures de f et f'
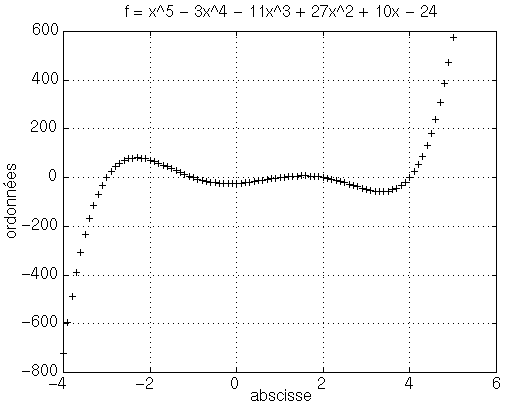
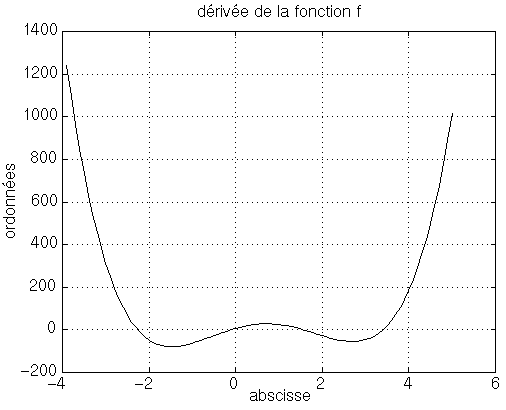
Les valeurs de x pour lesquels la fonction admet des extrema sont:
local =
-2.3000 -0.2000 1.5000 3.4000
Remarque: l'allure de la courbe représentant la dérivée montre que la fonction a des minima et des maxima locaux. La dérivée s'annule autant de fois que la fonction admet des minima et/ou des maxima.
Représenter les graphes des fonctions ci-dessous, ainsi que ceux de leurs dérivées premières et secondes dans l'intervalle [-10 10]. Déterminer également les points pour lesquels elles admettent des extréma. Utiliser un programme (fonction) en MATLAB afin d'accélérer la procédure.
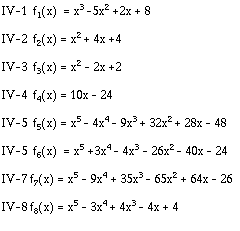

[ retour à la page principale | page précédente | page suivante ]