


Cette section permet d'étudier les différentes techniques de décomposition des matrices.
La décomposition LU permet de représenter une matrice carrée comme le produit de deux matrices triangulaires, l'une étant triangulaire supérieure et l'autre triangulaire inférieure (d'où le nom LU, L pour lower et U pour upper).
La décomposition QR permet de représenter une matrice quelconque A comme le produit d'une matrice orthogonale et d'une matrice triangulaire supérieure (Rappel: Une matrice Q est dite orthogonale si QQ'=I). On peut déterminer la décomposition QR en appliquant le processus de Gram-Schmidt sur les vecteurs colonnes de A afin d'obtenir une base orthonormale.
Il existe une autre méthode de décomposition appelé SVD, où décomposition par valeur singulière.
La matrice A est décomposée en trois matrices:
Soit les matrices A et B suivantes:
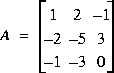
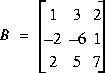
a - Décomposer A et B par la méthode LU.
b - Décomposer A et B par la méthode QR.
c - Utiliser la méthode SVD pour décomposer les matrices A et B.
On écrit ce qui suit dans une fenêtre MATLAB.
A = [1 2 -1;-2 -5 3;-1 -3 0]
[LA UA] = lu(A)
B = [1 3 2;-2 -6 1;2 5 7]
[LB UB] = lu(B)
[QA RA] = qr(A)
[QB RB] = qr(B)
[UA SA VA] = svd(A)
[UB SB VB] = svd(B)
On obtient les résultats suivants:
a - La matrice A
A =
1 2 -1
-2 -5 3
-1 -3 0
La matrice L de A
LA =
-0.5000 1.0000 0
1.0000 0 0
0.5000 1.0000 1.0000
La matrice U de A
UA =
-2.0000 -5.0000 3.0000
0 -0.5000 0.5000
0 0 -2.0000
La matrice B
B =
1 3 2
-2 -6 1
2 5 7
La matrice L de B
LB =
-0.5000 0 1.0000
1.0000 0 0
-1.0000 1.0000 0
La matrice U de B
UB =
-2.0000 -6.0000 1.0000
0 -1.0000 8.0000
0 0 2.5000
b - La matrice Q de A
QA =
-0.4082 -0.7071 -0.5774
0.8165 0 -0.5774
0.4082 -0.7071 0.5774
La matrice R de A
RA =
-2.4495 -6.1237 2.8577
0 0.7071 0.7071
0 0 -1.1547
La matrice Q de B
QB =
-0.3333 0.2981 -0.8944
0.6667 -0.5963 -0.4472
-0.6667 -0.7454 0.0000
La matrice R de B
RB =
-3.0000 -8.3333 -4.6667
0 0.7454 -5.2175
0 0 -2.2361
c - La matrice U de A
UA =
0.3387 0.0324 -0.9403
-0.8511 -0.4155 -0.3209
-0.4011 0.9090 -0.1132
La matrice S de A
SA =
7.2098 0 0
0 1.4070 0
0 0 0.1972
La matrice V de A
VA =
0.3387 -0.0324 -0.9403
0.8511 -0.4155 0.3209
-0.4011 -0.9090 -0.1132
La matrice U de B
UB =
0.3623 -0.0452 -0.9309
-0.4405 0.8719 -0.2138
0.8214 0.4875 0.2960
La matrice S de B
SB =
10.3031 0.0000 0.0000
0.0000 5.1804 0.0000
0.0000 0.0000 0.0937
La matrice V de B
VB =
0.2801 -0.1571 0.9470
0.7606 -0.5655 -0.3188
0.5856 0.8096 -0.0389
>>
Remarque: Les matrices A et B sont de rang 3 (cf: diagonales des matrices SA et SB)
X.1 - Dire si les matrices suivantes sont orthogonales ou non. Dites sur quelle(s) propriété(s) vous vous basez pour affirmer votre réponse.
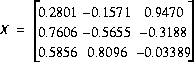
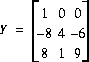
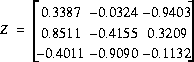
X.2 - Soit la matrice suivante:
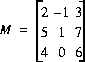
X.2a- Déterminer les matrices L et U de M.
X.2b- Déterminer les matrices Q et R de M.
X.2c- Déterminer les matrices U, S et V de M.

[retour ŕ la page principale | page précédente | page suivante]