Soit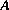 
une matrice carrée n x n et 
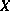un vecteur colonne ayant n lignes. 
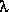étant un scalaire.
Considérons l'équation suivante:
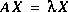(1)
Pour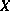 
non nul, les valeurs de 
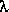qui vérifient cette équation sont appelées valeurs propres de la matrice 
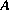. Les vecteurs correspondants sont appelés vecteurs propres.
L'équation (1) peut également être écrite sous la forme:
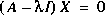
Un système d'équations homogène de cette forme a une solution non triviale si et seulement si le déterminant est nul, c'est-à-dire:
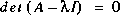(2)
(2) est appelée équation caractéristique de la matrice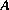 
. Les solutions de cette équation sont aussi les valeurs propres de 
.
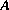Soit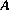 
la matrice suivante:
.
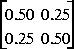
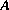Utilisant MATLAB on écrit ce qui suit:
A = [0.50 0.25;0.25 0.50];
[vecteurs_propres,valeurs_propres]=eig(A)
On obtient comme résultat:
vecteurs_propres =
0.7071 0.7071
-0.7071 0.7071
valeurs_propres =
0.2500 0
0 0.7500
On obtient deux valeurs propres qui sont 0.25 et 0.75.
À la valeur propre 0.25 correspond le vecteur propre
.
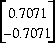À la valeur propre 0.75 il correspond le vecteur propre
.
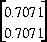Remarque: Soit
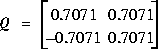
On a toujours QQ' = I. I étant la matrice identitée. eig produit des vecteurs unitaires.
Soit la matrice A suivante:
Répondre, en utilisant MATLAB, aux questions suivantes: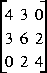
IX.1 Déterminer les valeurs propres de A et les vecteurs propres correspondants.
IX.2 Calculer det(A -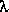 
I), vérifier que la relation obtenue est nulle pour chaque valeur de 
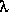trouvée en IX.1.
IX.3 Pour la matrice A donnée plus haut, montrer que:
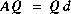
où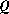 
est une matrice contenant les vecteurs propres en colonnes et 
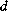la matrice contenant les valeurs propres correspondantes dans sa diagonale principale et des 0 partout ailleurs.
[retour à la page principale | page précédente | page suivante]