
UBI-INTERFACE
Contenu
But
Créer une interface
usager pour effectuer le contrôle du robot. De plus, pour ne pas
surcharger les fonctions exécutées sur
le robot, la plupart des traitements seront effectués sur l'ordinateur.
Dans ce qui suit, vous trouverez
le compte-rendu du développement de l'interface usager (UBINTERFACE)
ainsi que les différents
algorithmes nécessaires au contrôle de notre robot UBICOP.
Échéancier
L’échéancier est réparti sur
15 semaines. Les principales tâches effectuées à chaque
semaine sont résumées dans le tableau
suivant :
|
Étape
|
Date
|
Tâches effectuées
|
|
Semaine 1
|
7 Septembre
|
Création de l’entreprise, division des
tâches
|
|
Semaine 2
|
14 Septembre
|
Brainstorming sur les algorithmes de contrôle,
structure de base de l’interface usager
|
|
Semaine 3
|
21 Septembre
|
Début de l’Implémentation de
l’interface usager
|
|
Semaine 4
|
28 Septembre
|
Suite de l’implémentation de l’interface
usager
|
|
Semaine 5
|
5 Octobre
|
Début de l’intégration des algorithmes
de contrôle
|
|
Semaine 6
|
12 Octobre
|
Déverminage des algorithmes de contrôle
|
|
Semaine 7
|
19 Octobre
|
Rapport préliminaire
|
|
Semaine 8
|
26 Octobre
|
Déverminage des algorithmes de contrôle
|
|
Semaine 9
|
2 Novembre
|
Intégration du module de communication
série avec le UBICOP
|
|
Semaine 10
|
9 Novembre
|
Intégration d’une simulation virtuelle
|
|
Semaine 11
|
16 Novembre
|
Intégration et test de communication
série avec UBICOP
|
|
Semaine 12
|
23 Novembre
|
Détection et traitement des collisions
|
|
Semaine 13
|
30 Novembre
|
Intégration du positionnement et de
la communication RF
|
|
Semaine 14
|
7 Décembre
|
Tests finaux et rapport final
|
|
Semaine 15
|
14 Décembre
|
Présentation finale
|
La somme de travail effectuée
à chaque semaine correspond à environ 6h par personne, pour
un grand total de 180
heures. De plus, des réunions hebdomadaires ont eux lieu, d’une
durée moyenne de deux heures par semaine.
| retour au contenu |
Plan
général
La figure#1 représente
le plan général de notre programme en mettant en évidence
les principaux modules ainsi que les échanges d’informations entre
le robot et l'interface usager.
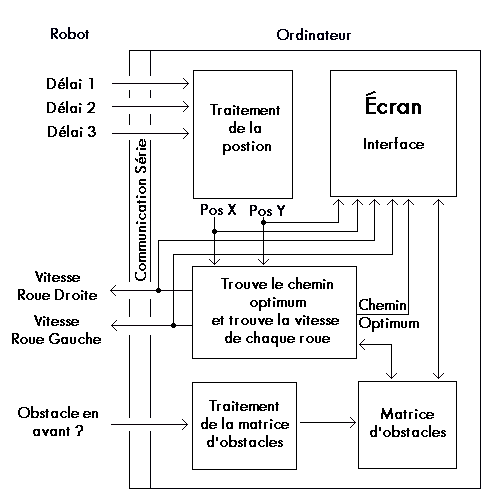 Figure #1 - Plan
du programme
Matrice
d'obstacles
Figure #1 - Plan
du programme
Matrice
d'obstacles
Nous commençons par
décrire la matrice d'obstacles, car tous les autres modules dépendent
de celui-ci.
La matrice d'obstacles représente
le terrain de 5 m par 5 m que nous avons divisé en carreaux. La
grandeur des carreaux peut
être changée facilement dans le programme. Nous avons choisi
cette grandeur en fonction de la précision que nous
avons pour la position du robot
et pour le positionnement des obstacles. La taille optimum des carreaux
est de 50 cm par 50
cm, ce qui est un bon compromis entre la précision du positionnement
spatial et l’exactitude des déplacements.
La matrice contient
la position des obstacles physiques ainsi que les obstacles virtuels que
nous pouvons ajouter à partir de 'interface. Chacun de ces deux
types d’obstacles possède son propre code dans la matrice de façon
à ce que l’on puisse les différencier dans la matrice. Sur
l'interface, les obstacles virtuels sont représentés par
des carrés noirs et les obstacles réels, par
des carrés verts. Pour faciliter le traitement dans les algorithmes,
nous simulons un obstacle autour de la matrice afin que
le robot ne sorte pas du terrain. De plus, pour éviter que le robot
passe trop près des obstacles, nous avons ajouté
une zone grise autour de chaque
obstacle.
| retour au contenu |
Traitement de la matrice
d'obstacles
Nous faisons une mise à
jour dynamique de notre matrice d'obstacles. Nous n'avons pas à
nous soucier des obstacles virtuels
placés par l'interface usager, car c'est l'usager qui va décider
s'il veut les enlever ou non. Cependant, il peut arriver
que sur le terrain, il y ait des obstacles physiques qui s'enlèvent,
s'ajoutent ou se déplacent. Il est donc primordial
de faire la mise à jour de notre matrice de façon dynamique.
Le positionnement des
obstacles physiques est possible grâce à l’information transmit
par le robot. Les routines de contrôle
implantées dans le robot vérifient à chaque cycle
si un obstacle lui fait face. Si c’est le cas, l’information nécessaire
est aussitôt envoyée
à l’interface via le lien série. Ainsi, nous pouvons vérifier
dans la matrice s'il y a un obstacle ou non et faire
les ajustements nécessaires.
Le robot utilise deux types
de détection. Le premier est réalisé par les infrarouges
qui permettent de voir les obstacles à tance(environ 30 cm). Le
deuxième type est les représenté par les détecteurs
de collision du robot. Dans les deux cas, il est
possible de savoir si l'obstacle est à gauche, à droite ou
au centre et il est ajouté en conséquence dans la matrice
d'obstacle.
| retour au contenu |
Communication
série
La communication entre le
robot et l’interface usager est possible via le lien série RS-232
du PC. La transmission se fait sur le
lien TX et la réception sur le lien RX. Il suffit de placer les
données dans les registres tampons du port et celle-ci sont
envoyées directement sur
le lien série.
Pour notre programme d’application,
nous effectuons le contrôle du lien série avec un objet de
la classe CSerialPort. À l’ouverture
de l’application, le port série est ouvert. Il est possible de modifier
la configuration de la communication série comme
le montre la
figure#2. En fait, les seuls
paramètres qui nous sont utile de modifier est l’identification
du COM et la vitesse
de transmission. En effet, chaque station de travail sur lesquelles nous
avons travaillé n’utilise pas nécessairement
le même COM, donc la possibilité
de modifier ce paramètre nous à été fort utile.
Pour ce qui est de la vitesse de transmission, l’équipe
qui s’occupe de créer le lien série sans fils n’était
pas en mesure de nous dire quelles seraient les vitesses supportées
par ce module, donc nous avons
conservé la possibilité de modifier ce paramètre.
Les autres paramètres sont fixés car on sait
que le robot communique toujours sur son port série avec la même
configuration.
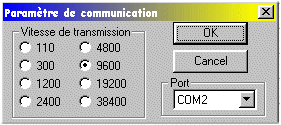 Figure #2 - Configuration
du Port Série
Figure #2 - Configuration
du Port Série
La gestion du port série
est prise en charge par un processus indépendant du logiciel d’application
(thread). Donc, lorsque des
données sont envoyées par le robot, ce processus envoie le
message WM_COMM_RXCHAR à l’application qui exécute
une routine de traitement en
réponse à ce message. C’est cette dernière qui détermine
l’action à prendre lors de la réception des
données. Les données susceptibles d’être reçues
sur le lien série, ainsi que les actions à effectuer sont
résumées dans le tableau
suivant :
|
Information reçue
|
Action à effectuer
|
|
Détection d’un obstacle
|
Mise à jour de la matrice et affichage
|
|
Délai entre les impulsions sonores
|
Validation des délais ;
Calcul de la position et du chemin optimum
;
Affichage du robot et du nouveau chemin optimum
;
|
|
Détection d’une collision
|
Mise à jour de la matrice d’obstacle
;
Calcul du nouveau chemin optimum ;
|
Pour ce qui est de la transmission,
les données sont placées sur le lien série par une
fonction WriteToPort qui reçoit en paramètres
les données à transmettre.
Le protocole de communication
utilise l’octet comme unité de base. Les données sont transmises
directement, sans aucun protocole
de communication. Ce point serait éventuellement à améliorer,
mais l’échéancier ne nous permet pas un tel
ajustement et la communication
a toujours été efficace de cette façon.
| retour au contenu |
Traitement
de la Position du Robot
Pour trouver la position
du robot, nous avions pensé à deux approches. La première
était de calculer la position en résolvant
des équations et l'autre était d'utiliser un outil intelligent.
Ce dernier est en fait un réseau de neurones qui,
à partir des trois délais
entre les impulsions sonores, fourni la position en 2 dimensions. Dans
les deux cas, le robot envoi
4 valeurs de compteurs à l’ordinateur à partir desquels les
délais sont calculés sur l'ordinateur pour qu'il puisse
faire le traitement de la position.
Le plan de la salle avec les haut-parleurs est montré à la
figure#3. La stratégie qui à été
adopté est celle du réseau de neurones, pour sa simplicité
et sa récision.
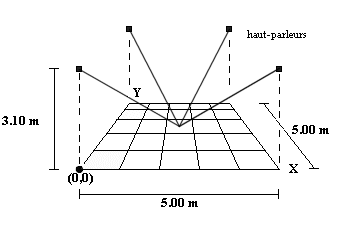 Figure #3 - Plan de
la salle avec les haut-parleurs
| retour au contenu |
Positionnement par
réseau de neurones
Figure #3 - Plan de
la salle avec les haut-parleurs
| retour au contenu |
Positionnement par
réseau de neurones
L’utilisation du réseau
de neurones, connu sous le nom de «Perceptron», rend très
facile le positionnement spatial. La méthode
consiste à recueillir une banque d’information relative à
la position, soit les trois délais entre les impulsions sonores,
et la position réelle
dans l’espace. Comme on sait que le robot se promène sur une surface
plane, sa position est ainsi réduite à
une coordonnée cartésienne à deux dimensions. Une
fois que le nombre de données amassé est suffisamment grand,
on entraîne
le perceptron.
L’entraînement du perceptron
consiste à lui donner en entrées les 3 délais et en
sortie la position cartésienne. Grâce à une
fonction de rétropropagation
de l’erreur, le réseau est ajusté pour obtenir une correspondance
entre les entrées et les sorties. En
lui fournissant ainsi une quantité suffisante d’informations, on
ajuste les paramètres du réseau et on peut par la suite
l’interroger. Nous lui donnons
les 3 délais en entrées et il nous fournit la position cartésienne
en sortie.
Revenons maintenant sur la
façon dont on a recueilli l’information nécessaire à
l’entraînement du réseau. Premièrement, nous
avions besoin de plusieurs mesures.
Pour effectuer celles-ci, nous avons positionné notre robot à
36 endroits équidistants sur le
terrain et demandé au robot de mesurer 3 délais. En fait,
le robot envoi 4 valeurs de compteur à partir des quels, l’ordinateur
trouve les 3 élais, tel que décrit précédemment.
Ces trois délais sont facilement mesurables par le robot, car nous
avons quatre haut-parleurs.
Le UBIP envoie des séquences de 4 impulsions (une dans chaque haut-parleur)
et chaque séquence est séparée
par un temps plus long que le temps qui sépare les impulsions. Ainsi,
le robot peut facilement savoir lorsqu'une nouvelle
séquence débute et ainsi mesurer les trois délais.
Nous ne transformons pas ces délais en distance car nous utilisons
directement les délais pour entraîner notre réseau
de neurones, tel qu’illustré sur la figure#4.
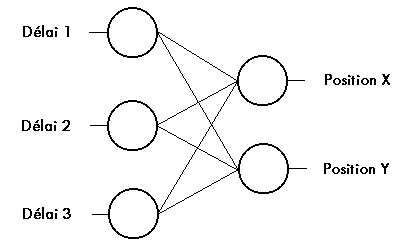
Figure #4 - Réseau
de neurone
Une fois bien entraîné,
le perceptron est en mesure de nous fournir d'une façon précise
et rapide la position du robot. Par
contre, cette précision est tout de même relative et nous
avons prévu un mécanisme de correction des erreurs. En
effet, dans le cas ou la position
calculée est irréaliste vue la vitesse de déplacement
du robot, nous comparons la nouvelle position
avec l'ancienne pour voir si le déplacement est réaliste.
Dans le cas contraire, la nouvelle position est tout simplement
ignorée et on attend l’envoie de la ochaine position pour modifier
le parcours du robot.
| retour au contenu |
Calcul du chemin optimum
Avant de diriger le robot, il faut savoir quel
chemin on veut lui faire suivre. C'est pourquoi nous avons fait une fonction
qui calcul le chemin le plus court entre le
robot et sa trajectoire. Cette fonction utilise la matrice d'obstacles,
la position du robot et la position d'arrivée.
Avec ces arguments, elle détermine le chemin optimum et retourne
à l'algorithme qui trouve la vitesse de
chaque roue (voir plus loin)la direction future, et le trajet complet calculé
est ainsi envoyé à l'interface usager. La figure #5
montre le résultat de l'algorithme du chemin
optimum. Il est facile de voir que l'algorithme fonctionne très
bien, et ce, dans des temps plus que
raisonnables, ce qui nous permettra d’avoir un
affichage en temps réel de la position du robot. Nous allons maintenant
voir plus en détails le fonctionnement de l'algorithme.
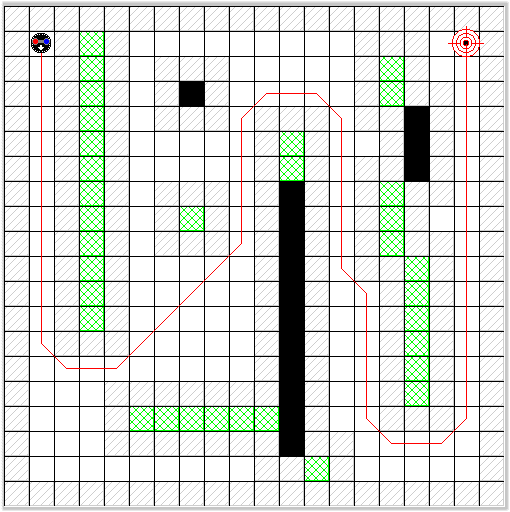 Figure #5 - Résultat
de l'algorithme du chemin optimal
Nous avons utilisé une
dérivée de l'algorithme de Dijkstra. Comme vous avez dû
le remarquer sur la figure #5, le
robot ne tourne qu'à 45 degrés. La raison est que de cette
manière, il est plus facile de faire les calculs du chemin
optimum et il sera plus facile
de diriger le robot. Nous avons donc défini 8 directions possibles
(voir figure #6). Pour
trouver le chemin optimum, nous vérifions tous les chemins possibles
entre le robot et la destination et nous choisissons
le chemin le plus court. En fait, l’algorithme arrête de calculer
les chemins aussitôt qu'il en trouve un qui
se rend à l'arrivée, car grâce au principe de l'algorithme
de Dijkstra, nous pouvons être certains que c'est le
chemin le plus court.
Figure #5 - Résultat
de l'algorithme du chemin optimal
Nous avons utilisé une
dérivée de l'algorithme de Dijkstra. Comme vous avez dû
le remarquer sur la figure #5, le
robot ne tourne qu'à 45 degrés. La raison est que de cette
manière, il est plus facile de faire les calculs du chemin
optimum et il sera plus facile
de diriger le robot. Nous avons donc défini 8 directions possibles
(voir figure #6). Pour
trouver le chemin optimum, nous vérifions tous les chemins possibles
entre le robot et la destination et nous choisissons
le chemin le plus court. En fait, l’algorithme arrête de calculer
les chemins aussitôt qu'il en trouve un qui
se rend à l'arrivée, car grâce au principe de l'algorithme
de Dijkstra, nous pouvons être certains que c'est le
chemin le plus court.
Pour nous aider à calculer
la distance, nous avons associé à un déplacement
horizontal et vertical une valeur de 1 et
à un déplacement en diagonal une valeur de 1.4 (les
déplacements diagonaux sont plus longs).
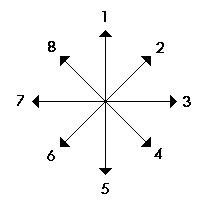 Figure #6 - Code des
directions
Figure #6 - Code des
directions
L’implantation de la dérivée
de l'algorithme de Dijkstra est assez simple. Nous utilisons une matrice
de chemins de même
dimension que la matrice d'obstacles pour garder les chemins déjà
trouvés. De plus, nous utilisons une
structure qui comprend la position en X, la position en Y, ainsi qu'une
variable Distance. Nous commençons par
le carreau de la matrice où se trouve le robot. On regarde toutes
les directions autours du carreau. Lorsque, pour
une direction donnée, il n'y a pas d'obstacle, nous insérons
dans la matrice de chemin, cette direction. De plus,
nous plaçons dans notre structure la position en X et la position
en Y, ainsi que la distance de 1 ou 1.4. Ensuite,
on copie les éléments de cette structure dans un monceau.
Un monceau est une structure de donnée en
arbre qui met toujours l'élément le plus petit à la
racine, soit la distance dans notre cas.
Après avoir terminé
le traitement avec le premier carreau, on prend un élément
du monceau, qui est en fait une de
nos structures. On a donc la position d'un carreau. Pour ce carreau, on
vérifie tous les carreaux autours de celui-ci.
Pour chaque carreau, on vérifie si celui-ci n'est pas occupé
par un obstacle, et on vérifie aussi si le chemin
pour se rendre à ce carreau
n'a pas déjà été trouvé en regardant
dans la matrice de chemins. Si ce n'est pas le cas, on
indique la direction dans la matrice de chemins. On met la position de
ce carreau dans une nouvelle structure et on
additionne 1 ou 1.4 (dépendant de la direction) à la variable
Distance du carreau d'avant. On met ensuite, cette structure
dans le monceau.
On répète ceci
jusqu'à ce que l'on arrive au point d'arrivé ou jusqu'à
ce que le monceau soit vide. Si le monceau est
vide, c'est qu'il n'y a pas de chemin possible. Si l'on arrive au point
d'arrivée, nous pouvons être certains que le
chemin est le plus court possible, car le monceau retourne toujours la
distance minimum pour arriver à un carreau.
Ensuite, pour trouver
le chemin à suivre, nous n'avons qu'à commencer à
partir de la position d'arrivée dans la matrice de
chemins et suivre la direction inverse qu'indique le code de direction.
| retour au contenu |
Direction du Robot
Maintenant que nous connaissons
le chemin que doit suivre le robot, il ne nous reste simplement qu’à
demander au robot de
suivre ce chemin. Nous avions pensé à plusieurs solutions
pour remédier à ce problème. L'une d'elles est de
faire une fonction
sur le robot qui demanderait à celui-ci de tourner d'exactement
45 degrés et d'avancer de 1 ou 1.4 selon la direction.
Ceci implique que le robot doit
être extrêmement précis et il n'y a pas de place pour
des perturbations extérieures. De plus, cela
implique aussi que le robot doit arrêter pour tourner.
Une autre solution, celle
que nous avons adoptée, est de calculer dynamiquement la direction
du robot au fur et à mesure que
celui-ci se déplace. En effet, nous recalculons la position du robot
ainsi que sa direction à chaque fois qu'il change de
carreau dans la matrice. Donc,
le robot va pouvoir effectuer les modifications nécessaires s'il
y a des perturbations extérieures
qui le font dévier de sa trajectoire (ex : une roue qui tourne dans
le vide).
La figure #7 montre
le diagramme du fonctionnement de l'algorithme qui s'occupe de diriger
le robot.
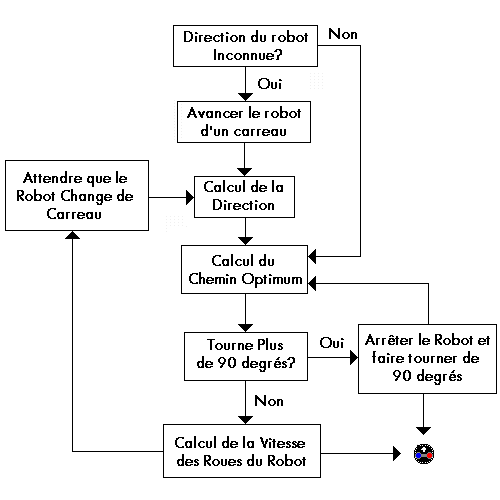 Figure #7 -
Diagramme de l'algorithme qui dirige le Robot
Figure #7 -
Diagramme de l'algorithme qui dirige le Robot
Au début, si on ne
connaît pas la direction du robot, on fait avancer le robot de 1
carreau dans la matrice. Ainsi, on peut
connaître la direction du robot. Ensuite on calcule le chemin optimum.
S'il faut faire tourner le robot de plus de 90
degrés, nous arrêtons le robot et nous le faisons tourner
de 90, -90, 135, -135 ou 180 degrés. Cependant, lorsque
l'angle est inférieur
à 90 degrés, nous ne voulons pas que le robot s'arrête
pour tourner. Pour ce faire, lorsque l'on voudra
tourner à gauche, nous mettrons la vitesse de la roue gauche à
1 et l'autre à 2. Ainsi, le robot va tourner sans
arrêter. De plus, lorsqu'il
va changer de carreau dans la matrice, on pourra détecter si le
robot est dans la bonne direction. S'il
l'est, nous n'aurons qu'à mettre les deux roues à la même
vitesse pour qu'il avance droit. Ainsi, en jouant avec la
grandeur des carreaux de la matrice,
nous pensons pouvoir faire une sorte d'asservissement qui permettra au
robot d'avancer
sans trop osciller.
| retour au contenu |
Interface
usager
L'interface usager, tel que
nous l’illustre la figure #9, possède plusieurs caractéristiques
:
-
Affichage en temps réel
de la position du robot, de sa destination et du chemin qu’il doit suivre
;
-
Affichage de la position du contrevenant
;
-
Affichage de l’information reçue
et transmise sur le port série ;
-
Affichage de la tension des batteries
;
-
Affichage de la vitesse de chaque
roue du robot.
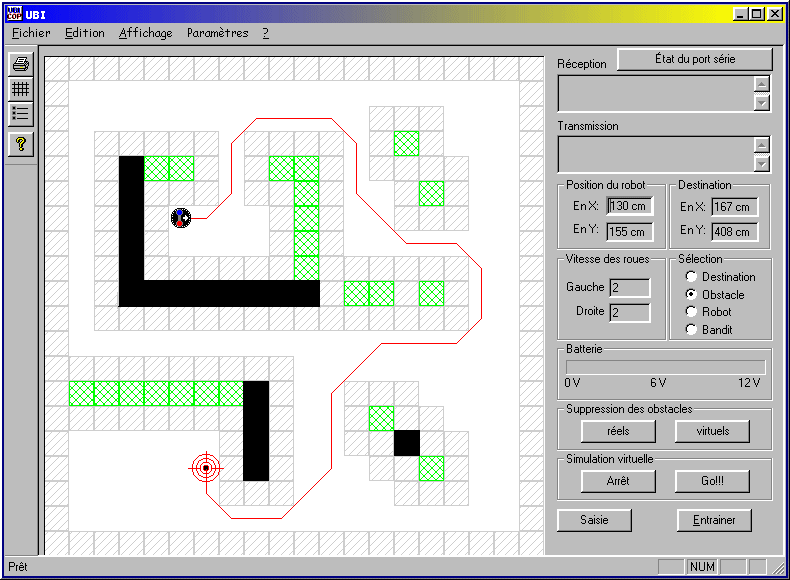 Figure #9 -
Interface usager
Figure #9 -
Interface usager
Pour ce qui est de la direction
du robot, on peut la repérer facilement à l’aide de la flèche
situé sur le robot virtuel de
l'interface. Le contrevenant
est représenté par une petite voiture sport rouge (figure
#10).
 Figure #10 -
Contrevenant
Figure #10 -
Contrevenant
Les différents contrôles
qu’on retrouve sur l’interface nous permettent d’effectuer plusieurs tâches
:
-
Sélection de la position
virtuelle du robot (pour fin de test) ;
-
Sélection de la destination
;
-
Sélection de la position
du contrevenant ;
-
Démarrage/arrêt
de la simulation virtuelle ;
-
Démarrage/ arrêt
de la simulation en temps réels ;
-
Vérification de l’état
du port série ;
-
Suppression des obstacles virtuels/réels
de l’environnement du robot.
Tous ces contrôles servent
évidemment à configurer les différentes simulations.
Lorsqu’une de celle-ci est amorcée, on
peut voir le robot suivre le chemin tracé, et celui ci se recalcule
à chaque fois que le robot se déplace, permettant
ainsi une adaptation dynamique
du robot dans sa trajectoire.
Il est également possible
de configurer le port série grâce à une boite de dialogue
(voir figure #2) qui affiche les paramètres,
tel que mentionné dans la section Communication série.
| retour au contenu |
Assemblage
des modules
Nous avons mit la communication
série, l'affichage de l'interface ainsi que l'algorithme qui trouve
la vitesse des roues dans
des processus(thread) séparés. De plus, nous avons mit des
sémaphores pour les variables qui sont partagés par
les processus afin que nous n'ayons
pas de problèmes.
Comme vous avez pu le constater,
ce groupe à construit l'interface et les algorithmes en supposant
que les autres parties du
projet marcheraient plus ou moins. En effet, l'interface permet de mettre
des obstacles virtuels au cas où la détection
d'obstacle ne marcherait pas.
Les grosseurs des carreaux de la matrice peuvent varier selon la précision
du positionnement. Une vérification du positionnement est faite
par l'interface pour s'assurer que la position du robot est réaliste.
L'orientation du robot
est vérifiée à chaque fois qu'il change de carreau
dans la matrice. Le trajet optimal est recalculé périodiquement
pour contrer les
influences extérieures qui pourrait faire dévier le robot.
Ce n'est pas par manque de confiance auprès des autres
groupes que nous avons agit ainsi,
mais pour facilité l'intégration des différentes partie.
| retour au contenu |
Résultats
Malheureusement, les résultats
obtenus sont loin d'être ceux escomptés. Le robot à
de grandes difficultés à suivre le chemin
optimum. Cela s'explique par le fait que le délai entre l'envoie
des vitesses et l’exécution de la commande par le
robot est trop long. Il faut
environ deux secondes pour le robot pour trouver sa position. Durant ce
temps, il avance de beaucoup
et lorsqu’on lui envoi une commande, elle est pour ainsi dire, désuète.
Donc, le robot tourne soit trop loin, soit trop
longtemps et il tourne donc autour de l'obstacle. Cependant, il fini souvent
par atteindre son but, ce qui est le principal.
De plus, nous avions de la
difficulté à faire tourner le robot sur lui-même. On
voulait une fonction qui fait tourner le robot d'environ
180 degrés mais le robot n'était vraiment pas assez précis
(les encodeurs ne marchaient pas bien) et il ne tournait
jamais du même angle.
Le temps est le plus grand
facteur qui a joué contre nous. Notre algorithme du chemin optimum
fonctionne très bien et le positionnement aussi. Avoir eu plus de
temps, nous aurions pu améliorer de beaucoup la trajectoire suivit
par le robot. Nous
aurions pu aussi inclure l'odométrie pour contrer l'effet du délai
dans le calcul de la position par le robot.
| retour au contenu |
Conclusion
Nous pouvons dire que nous
avons rempli notre mandat même si nous n'avons pas atteint notre
objectif qui était de conduire
le robot à un point en suivant le chemin optimum. Les résultats
sont quelques peu décevant, mais l'expérience
acquise durant ce projet compense
grandement cette lacune. Il faut toutefois préciser que le
robot se rend quand même au
point de rendez-vous, ce qui était une exigence du projet.
Pour ce qui est des autres
exigences, tels que la détection des collisions et la détection
des obstacles, les résultats sont très ppréciables.
Le robot détecte bien les obstacles et lors d’une collision, il
passe en marche arrière, recule d’une courte distance
et peut ainsi continuer son chemin en évitant l’obstacle détecté.
L’affichage de la tension des batteries n’a pas été
réalisé, mais l’interface dispose d’un mécanisme prévu
à cet effet.
Le projet en est donc encore
à l’étape du prototype. Plusieurs possibilités sont
envisagées pour remédier aux divers problèmes
mentionnés précédemment, mais l’échéancier
ne nous permet pas de continuer le développement.
Néanmoins, le logiciel
d’application est disponible dans la section téléchargement,
et est totalement opérationnel.
Adressez vos commentaires,
questions ou autres, à un des deux responsables de la section Interface
usager :
Sébastien Pouliot :
poulio00@gel.ulaval.ca
Pierre Martin-Dumont : martin01@gel.ulaval.ca
| retour au contenu |
Informations
supplémentaires










